我正在拍攝一個球體（一個球）：在同一張照片中，我還放置了一個標尺。球和標尺在同一平面上。即標尺的放置應使其與球的中心對齊。
我嘗試通過尺子預測球的圖像大小：
結果是球的圖像大於應有的圖像根據我的身體測量。顯然圖像中存在問題。你們能想到這個原因嗎？
我正在使用帶閃光燈的FL 5.5鏡頭。 （此鏡頭的畸變非常小。）
如果我使用FL為4.5的其他鏡頭，這個問題不太明顯。 FL不知何故有影響，但我不明白是什麼。
要使圖像成為有效的測量工具，必須滿足兩個條件：
一個標準很容易驗證，兩個物體都坐在平坦的表面上嗎？與相機和物平面之間的距離相比，任何物體的深度都大嗎？例如：從10英寸開始的1英寸球可能會產生明顯的效果，從數百英寸處成像的1英寸的球可能不會產生明顯的效果。
第二個條件稍微複雜些。將兩個標尺彼此垂直放置在圖像平面上將允許驗證此標準。計算標尺兩端每個標尺的像素。如果數量相等，則該標尺與圖像平面平行。比較標尺之間的測量結果，以驗證您的像素是否為正方形。
我創建了以下圖像來說明當對像從測量平面明顯突出時會發生什麼情況。在我的示例中，球填充了圖像的高度。標尺上圖像的高度為1.35單位。觀眾然後假設球也是1.35單位寬。這不是真的。如果放置在離鏡頭足夠近的地方，則可以使任何物體充滿邊框。
基本問題是標尺和球的水平線不在同一平面上。想想看一個球體。如果您從遠處看，幾乎可以看到一半。當您靠近時，您會看到越來越少的球體，因為地平線向您移動。您站在地球上是從非常近端到極端看球的一個很好的例子。您能從站立的地方看到一半的星球嗎？當然不是。即使從高樓大廈或飛機上，您仍然只能看到一小塊圓形的地球。如果您將標尺放在這個小的圓形小塊上並假設您可以看到地球的整個直徑，那麼您將對整個地球的大小有一個非常錯誤的認識。
您正在遇到同樣的問題，但沒有那麼強烈。您在照片中看到的球體的圓盤小於球體的一半。假設您正在從北極上方俯視球體。您看到的地平線比赤道更近。不僅會給您錯誤的球體直徑概念，而且地平線比標尺更靠近相機，因此您甚至無法正確測量它。
要最大程度地減少這種影響（您永遠無法完全消除它），盡可能遠地使用，並使用更長的鏡頭進行補償。
我認為這是一個數學角度問題。
球是3維對象，標尺（基本上）是2D對象，因此它們之間的關係取決於球的精確對齊方式和尺子。
讓我們說，您的標尺水平位於球的背面（從攝像機的角度看），那麼與標尺刻度相比，球看起來會比實際尺寸大。
但是，這不僅如此簡單-因為您的鏡頭是廣角鏡頭，所以我認為您的相機距離拍攝對像很近，因此您會遇到一種我不記得...這個名字的現象（我有多有用？ ？!!），由此光線進入透鏡的角度使球充滿了比標尺刻度所建議的更多的幀。
我想說的是您正在觀察變形，這是您嘗試過的一個非常不錯的實驗。
這類似於直線出現彎曲和角度變形的情況。
根據可使用的焦距，應該可以通過將球體放置在圖像的中心或邊框附近來觀察不同的差異：希望邊框附近的失真會更大。因此，也許您在中心看到的差異只是少量像素，當將球體放置在視野邊界附近時，差異會更大。
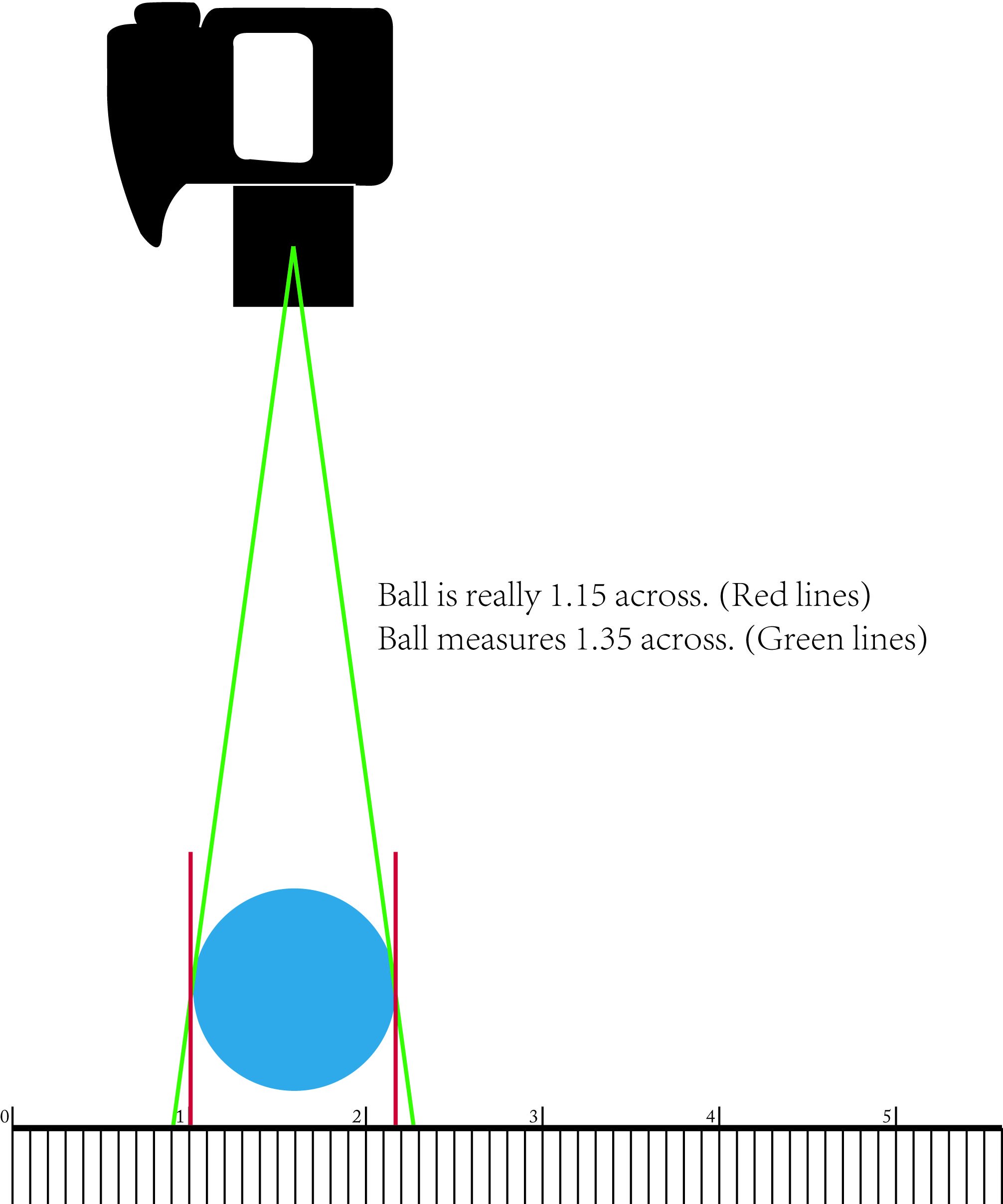
這有一個簡單的數學/幾何解釋：在任何基本幾何書籍中，您都會發現與圓的切線垂直於從圓的中心到切線與圓周接觸的點的線。 / p>
在此之後，接觸圓周的直徑極限的切線將完全平行，也就是說，這些線在任何點都不會收斂。
如果在圓周外的一個點ara（也與圓周相切）收斂，則接觸點將不與圓周的中心對齊，如果將兩個接觸點與中心連接，則會得到兩條線形成一個角度。如果將會聚點移到更靠近圓周的位置，則前面提到的角度會更銳利。
如果對線進行延長直到它們與圓周的直徑相交，您會發現相交點即使不在很小的範圍內，也不會落在圓周上，而是落在圓周上。
此外，如果您測量接觸點之間的距離，您會發現它實際上小於圓周的
直徑。
當您看到球體的圖像時，它的邊界是由切線從球切向傳播的光線形成的，這會聚聚一個會聚點（可能在透鏡內部），因為存在一個會聚點，您會在2D上下文中獲得與上述相同的效果，但從收斂的角度來看。
另一種思考方式是：如果這些光線變成固體，它們將符合圓錐形，直到將無法觸摸球的直徑，唯一可以通過其直徑接觸球的球會是管子。
不可避免的是看到的效果，它與焦距本身無關，而是與相機到物體的距離有關。如果您離物體更遠，則切線的角度會變得更銳利，也就是更接近於平行，從而將您所描述的差異最小化。
（對不起，我無法使用繪圖目前使用的工具。用圖形更容易解釋）