我知道增距鏡會減少到達照相機中的膠卷或傳感器的光量，因此，您會聽到人們在諸如“使用2倍增距鏡將300mm f / 2.8變為600mm f / 5.6“。
鑑於光圈在物理上沒有什麼不同，我想知道這如何影響景深（以及相關的散景效果）。人們應該說，景深保持不變，並且圖像只是被裁剪。
人們所說的僅僅是這些事情中的另一件事，它可能會方便進行曝光計算或是否存在實際產生的圖像有變化嗎？
TL; DR版本：增距鏡在任何給定距離都不會影響景深。他們從字面上將300 f / 2.8鏡頭轉換為600 f / 5.6鏡頭。無論是否進行遠距轉換，任何600 f / 5.6鏡頭都將具有與300 f / 2.8鏡頭相同的景深。
對於景深之間的關係存在很多困惑，光圈，光圈和焦距。實際上，這非常簡單：
由視在直徑，我的意思是前元件不受孔徑限制的寬度。
實際上，通過觀察鏡頭的前部，您可以看到表觀直徑的大小。
光圈，焦距和表觀鏡頭直徑之間的關係如下：
（以毫米為單位的光圈大小）=（焦距（mm）÷（光圈）
例如：
現在，回到景深。景深是聚焦距離之前和之後的距離，仍然是“可以接受”的聚焦距離。由於可接受的模糊程度因人而異，因此分析景深的更好方法是通過混亂圈。
下面是Wikipedia頁面上的方便圖片混淆圈：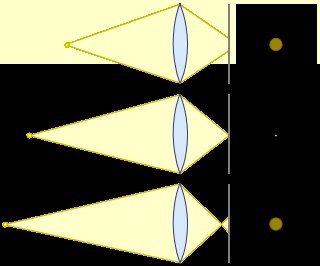
混淆圈是傳感器上被單點光擊中的區域。如果您位於焦點平面的前面或後面，那麼混亂的圈子會更大。在焦點平面上，混亂的圈子（理想情況下，但實際上從不）為零。
從焦點平面移開時，您的混亂圈增長多快只是一個因素：最寬的會聚線之間的角度（表觀鏡片尺寸的邊緣） 。現在，這意味著幾件事：
相反，這也揭露了一些關於景深的普遍看法：
拍攝兩張照片：一張為35mm f / 1.8，另一張為210mm f / 11。現在，裁剪35mm圖像，使其具有與其他圖像相同的視野。它們將具有幾乎完全相同的景深。你去了：
景深是您所舉示例中F / 5.6鏡頭的景深。
是的，光圈沒有物理變化。但是，光圈與焦距的比率增加了。
因此，到達傳感器的光線不會那麼傾斜。這樣可以增加景深。
不能在Itai關於發生的事情的出色解釋中添加任何內容，但是我將通過 Reducio ad Absurdum引入證明：
假設使用擴展的增距鏡焦距，因此可以減少光線，但不影響景深。除了製造600 f / 5.6的產品外，製造商還可以採用現有的300 f / 2.8的設計，並在同一機身中集成一些增距鏡。然後，他們將能夠提供兩種版本的600mm鏡頭，它們的曝光方式完全相同，但是一個版本的DOF為600 f / 5.6，另一個版本的DOF為600 f / 2.8。
他們還可以將150 f / 1.4的300 f / 2.8替換為裝有望遠鏡蓋的電視，並能夠提供600版本的3種版本，具有不同的景深等。
最終，您到達鏡頭的景深極小，但仍然像5.6一樣，這顯然是荒謬的，因此最初的主張（通過望遠鏡確定DOF不變）必須是錯誤的。
增距鏡只是像放大鏡一樣散佈鏡頭的圖像。它僅通過裁切（偽裝較大的聚焦距離）來更改幀，並通過對更多像素使用等量的光來更改照明級別。它不會改變原始鏡頭的其他任何內容，例如DoF或聚焦距離。
您感到困惑：
鑑於光圈在物理上沒有什麼不同，我想知道這如何影響景深（以及相關的散景效果）。合理的是，景深保持不變，而圖像僅被裁剪。
裁剪圖像僅在物理上打印時才保留相同的景深，從而導致一張較小的紙，以與原始紙相同的方式查看。一旦採用任何形式的放大以更好地查看細節，景深（通過仔細檢查即可辨認的通過不鋒利度的散佈盤定義）就會變小。唯一的例外是當已經有絕對的限制因素可見時，例如膠片顆粒或像素大小。
法蘭側增距鏡不會改變入射光瞳的大小，因此可以在相同場景下工作，但是整個傳感器分佈的作物較小。這使它每個像素的光更少（因此是光圈數的兩倍），但是由於傳感器像素更多，“混亂圓”的大小只有一半，因此景深只有一半。除非鏡頭的光學質量已經達到極限，並且其他像素無法提供任何其他信息。
濾鏡側增距鏡是另一回事，因為它確實放大了入口的尺寸。瞳孔，因此通常保持相同的光圈數。因此，通過在同一傳感器上分辨的較小作物以及較大的入射瞳孔看著景物，景深就會變小。
我將回答兩個問題，一個是您問的，另一個也是您應該問的。我還將介紹各種不同的場景（相同的主體距離而不進行裁剪，相同的主體距離進行裁剪以及相同的取景）。
增距鏡如何影響景深？
讓我們來看看這個。景深為：
DoF = 2 * x_d ^ 2 * N * C / f ^ 2 其中 f 是焦距， C 是混亂的圈子， N 是光圈數， x_d 是被攝體距離。如果被攝體距離保持恆定，並且您沒有決定由於裁剪較少而需要增加 C ，那麼焦距加倍也會使光圈數增加一倍，但是 C 保持不變。因此，景深將被增距鏡減半。 （如果由於減少了裁剪而增加了 C ，則景深將保持不變。）
但是，有時您希望保持相同的幀。然後，焦距加倍將對應於被攝體距離加倍。因此， x_d ^ 2 / f ^ 2 保持恆定，而 C 也保持恆定。但是，焦距增加一倍會使 N 增加一倍，因此景深將在等構圖的情況下增加一倍。
因此， TL; DR： b >這取決於您是否通過更改被攝體距離（不同的DoF）來保持相同的取景，是否進行裁切（相同的DoF）或是否接受更長的焦距才能獲得不同的圖像（不同的DoF，但方向相反）。
您還應該問：
增距鏡如何影響背景模糊？
這很容易。背景模糊光盤大小（假設背景為無窮大）為：
b = f * m_s / N =（f / N）* m_s
光圈開口 f / N 由增距鏡保持。 m_s 是對象的放大倍數，即傳感器上的對像大小除以其實際大小。如果保持相同的幀， m_s 保持恆定，因此，在相同的幀中，背景模糊光盤大小是恆定的。
但是，如果不保持相同的幀，則2倍增距鏡將 m_s 加倍。因此，您將獲得更多的背景模糊。
但是，如果您保持被攝體距離不變，並且已將原始圖像裁剪了2倍，並決定由於增距鏡而不再需要裁剪，那麼增距鏡將 m_s 加倍，但由於裁切較少，實際使用的傳感器片的寬度/高度/對角線也加倍，因此模糊光盤尺寸佔實際使用的傳感器片對角線的百分比保持不變。
因此， TL; DR： b>在這裡再次取決於是否通過更改被攝體距離（相同的模糊），裁切（相同的模糊）還是保持相同的取景無論您是否接受更長的焦距，都會得到不同的圖像（不同的模糊度）。
公認的答案非常明確。這也是錯誤的。首先讓我們在這裡說明正確的地方：
TL; DR版本：增距鏡不會影響任何給定距離的景深。
錯誤。 / p>
他們從字面上將300 f / 2.8鏡頭轉換為600 f / 5.6鏡頭。
正確。
任何600 f / 5.6鏡頭（無論是否進行遠距轉換）將具有與300 f / 2.8鏡頭相同的景深。
錯誤。
深度視場由焦距和鏡頭前部元件的視在尺寸決定。
部分正確，部分錯誤。場景的幾何形狀及其與景深的關係取決於鏡頭入射光瞳的視在尺寸。入射光瞳是當看著前透鏡時所看到的光圈的表觀尺寸。
其直徑可以通過將焦距除以光圈數來確定。我們在公認的答案中犯了一個基本錯誤：答案假設場景幾何是影響景深的唯一因素。不是。景深定義為您可以檢測到不清晰的距離，而不清晰則通過“混亂圓”標准進行定義。如果您使用相同的投影介質（相同的膠片或傳感器），並以一定的比例查看結果，則介質的分辨率將定義混亂的圓，則場景再現的放大倍率與所得到的景深非常相關。
如果在40MP全畫幅傳感器上使用具有相同設置的相同鏡頭，則其景深將為（假設鏡頭產生像素級清晰度）為10MP的一半全畫幅傳感器，但與10MP作物因子2傳感器的傳感器相同。忽略像素化，部分圖像將無法區分。
類似的法蘭式增距鏡保留了圖像的幾何形狀：只要忽略像素化，作物就無法區分。但是，正是像素化定義了混亂的圓，因此使用2倍增距鏡時，通常會獲得一半的景深，因為作為混亂圓的主要起因的像素現在覆蓋了原始像素上的細網格
與景深相反，根據像素大小量化背景模糊似乎是沒有意義的，因為它的大小與被攝對象特徵的大小或幀大小的相關性更大。增距鏡不改變與被攝體特徵的關係，相對於畫框，其範圍加倍，這意味著與完成圖像有關的模糊度會擴大。
簡而言之：事物複雜且雖然還不直觀，但是在將增距鏡加入方程式之前已經如此。由於這種複雜性，您需要非常仔細地指定所要查詢的值，因為它們通常在口語中經常互換使用，但是在查看場景幾何圖形，圖像幾何圖形和介質分辨率時，行為方式卻大不相同。 / p>