這個問題的答案不是&傳感器在實踐中可以做的是什麼，而是光學系統在理論上可以做的。這裡的“理論上”是指“在完美的觀察條件下，完全沒有大氣乾擾”。我懷疑（但不確定）對於像攝像機鏡頭這樣的相對較小的光學系統，以及相對較好的大氣條件，大氣不會受到限制。它限制了像望遠鏡這樣的大型光學系統，儘管有一些非常令人驚奇的技術被稱為“自適應光學”，當然，涉及捆綁在望遠鏡上的激光可以解決這一問題。同樣，您也可以在太空中。

因此，答案是給定了對波長為λ的前元素直徑為d的光學系統的角分辨率的限制。通過

Δθ= 1.22λ/ d

1.22的數字軟糖係數可以根據分辨率的含義進行微調，但調整幅度不大。該限制稱為光學系統的衍射限制。

如果Δθ小（如果您有任何合理的透鏡，則為θ），則相距一段距離然後該長度您可以解決的是

Δl= 1.22rλ/ d

對此進行重新排列

r =Δld /（1.22λ）

這是前端直徑為d的光學器件在λ波長下可分辨Δl的範圍。

綠光的波長約為500nm，假設您需要Δl= 1cm就能看到一張臉的所有細節（我不知道您是否可以以此分辨率識別一個人，但您可以知道它是一張臉）。

輸入這些數字，我們得到r = 16393 d，其中r和d均為厘米。如果d為5厘米，則r小於1公里。這意味著無論如何放大，如果您的前部元素的直徑為5cm，這就是該距離下分辨率的極限：如果您放大圖像，則只是在放大模糊。 / p>

在另一個答案中，有人提到了Sigma 150-600mm變焦鏡頭：正面元件的尺寸似乎為105mm。這給出了r = 1.7km，因此該透鏡可能接近或實際上受到衍射的限制：它不僅能夠分辨，而且在物理上也是可能的。

還提到了這也許佳能5200mm鏡頭很難找到規格，但是我發現某個地方聲稱其整體尺寸為500mm x 600mm x 1890mm：如果這些尺寸正確，那麼前元件的直徑不超過500mm，因此我們得出該鏡頭的r = 8km左右。因此，尤其是它不會讓您看到數十英里之外的面孔，這是炒作所暗示的意思。

您當然可以將此公式用於任何目的：例如它告訴您為什麼您無法使用任何可行的望遠鏡從地球上看到阿波羅登陸月球的地點：如果您想在月光下分辨約350,000英里的月球上3m的綠光，您需要一個帶有直徑約80m。有正在建造的望遠鏡將具有超過30m的鏡子，但這並不是特別接近80m。

還有另一個與“您能看到多遠”無關的概念，這是“你能在地球上看到多遠？”。同樣，這個問題的答案過於簡單。如果您假設

• 地球是一個完美的球體；
• 沒有大氣層引起的折射；
• 大氣層實際上是缺少或完全透明；

然後對這個問題有一個簡單的答案。

如果您在表面上方 h1 的高度（記住，它是一個非常光滑的球體），並且您想在表面上方 h2 的高度看到某物，那麼可以看到的距離就是

d = sqrt（h1 ^ 2 + 2 * R * h1）+ sqrt（h2 ^ 2 + 2 * R * h2）

其中R是地球的半徑，“ sqrt”表示平方根，所有距離均應使用相同的單位（以米為單位）。如果R與h1或h2（通常是！）相比較大，則可以近似為

d = sqrt（2 * R * h1）+ sqrt（2 * R * h2）

此距離是僅掠過地平線的光線的長度，因此此公式還告訴您到地平線的距離：如果您位於表面上方的高度h，則到地平線的距離是

sqrt（h ^ 2 + 2 * R * h）

或者如果h比R小（通常，除非您在太空中，否則通常為true）

sqrt（2 * R * h）

在現實生活中，大氣折射確實很重要（我認為這通常會使地平線更遠），大氣層並不是完全透明的，而地球是

但是昨天我花了一個小時的時間觀察著島嶼逐漸消失在地平線下，因為我駛離了它們，所以我想我會添加一個，這是我自己在船上的娛樂活動。

如果您只是想要帶有常用鏡頭和分辨率的視覺示例，請訪問以下網頁：“ 識別或識別面部的指南：分辨率，焦距和百萬像素”提供了許多示例。

Axis Communications稱之為像素密度模型：

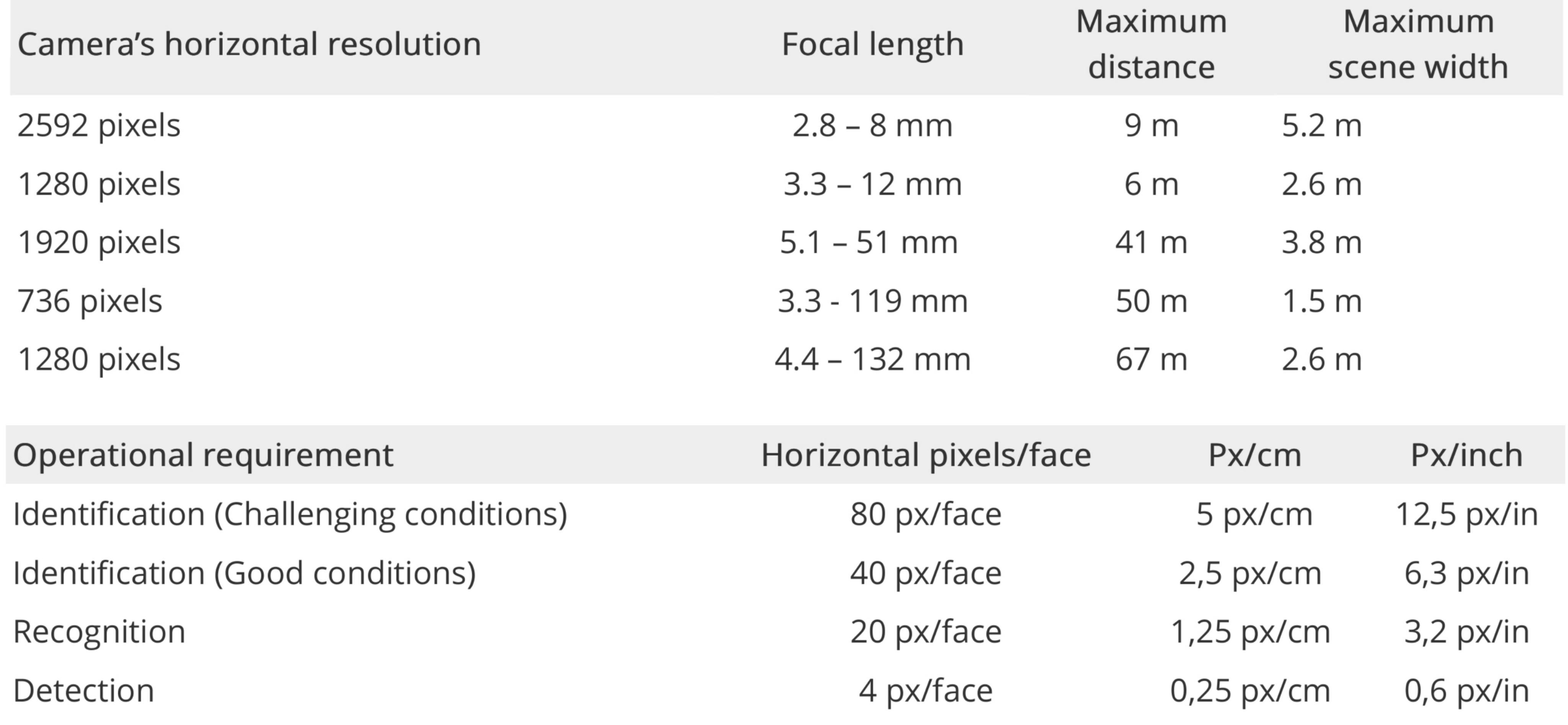
_{最大距離示例用於識別（500像素/米或80像素/面）。軸定義了檢測，識別和識別的要求。 sub>}

有許多要計算的因素：前後照明，甚至角度，霧或煙，顏色，距離，鏡頭出現在面部（中心或角落），鏡頭質量，傳感器質量，相機角度，人物運動（或相機抖動），圖像壓縮等；這就是安全攝像機製造商創建具有保證識別性能的圖表的原因。

在完美的條件下，您應該期待更多。同樣，如果存在一個已知人物列表，可以將圖像與一個圖像進行比較，則通常可以說它是一個圖像而非另一個圖像。現代軟件甚至可以分析以不同角度拍攝的多張圖像，並提供具有增強分辨率的最終圖像。所有這些因素使精確的數學計算不太有用。

另請參見“發光景觀”文章：“ 傳感器能分辨出透鏡嗎？”和《埃德蒙光學成像資源指南》中的“ ”部分4.3解釋：

“成像系統無法可靠地成像尺寸為12.4μm的物體特徵的結論與我們的應用筆記 Resolution中的方程式正好相反，因為數學上物體會掉落該矛盾突出表明，一階計算和近似值不足以確定成像系統是否可以達到特定的分辨率；此外，奈奎斯特頻率計算並不是奠定基礎的堅實指標系統的分辨率，僅應作為系統限制的準則。”。

儘管進行了所有計算，但並不能完全反映真實情況。

用望遠鏡看到的最遠的（巨大）物體之一是 134億光年（地球的年齡是 4.54±0.05十億年之久），但它是人類f大小的物體在很遠的地方 都看不到ace。

這裡有 8000 個圖像要使用佳能7D和尺寸為600,000像素的400mm f / 5.6鏡頭製作出巨大的可縮放圖像，如果以照片分辨率打印，則尺寸為50米x 100米：

這就像擁有一個巨大的變焦鏡頭並增強圖像以提高分辨率一樣。您幾乎看不到最遠處的建築物，這些建築物被大氣所遮蓋。

視頻中顯示了有史以來最大的鏡頭（僅製作了3枚）：“ 5200mm佳能鏡頭世界的MOST功能強大的超級遠攝EF FD（更新後的上傳）”，在此Petapixel文章中對此進行了描述： “ eBay上的5200mm佳能佳能鏡頭”，其最小聚焦距離為393ft / 120m，重量為220lb（100kg），沒有支架。它能夠拍攝18到32英里（30公里到52公里）遠的物體的照片，這當然取決於物體的大小。

以下是視頻的屏幕截圖：

_{在第一張照片中，建築物的頂部與建築物的頂部大約相同。女士的手在最後一張特寫照片中。 sub>}

這取決於您使用的鏡頭。

我在尼康D850上有一個sigma 150-600mm鏡頭，我可以安全地識別1.2公里範圍內的人物

有一個CANON 5200mm鏡頭，可達到更長的距離：

在日本製造的5200mm Prime具有極好的變焦距離。它旨在聚焦於18到32英里外的物體。基本上，如果5200mm Prime的功能強大得多，那麼地球的曲率就會開始影響結果

https://www.geek.com/gadgets/canons- 5200mm-prime-lens-is-super-rare-and-requit-massive-1534367 /

檢查鏈接中的視頻以進行簡短演示。

我用Nikon D750和Tamron 150-600 mm在600 mm，f / 11、1 / 2000 s和ISO 1600上帶了這個手持式（或者可能是從平坦的平台上獲得了支撐，但沒有三腳架）。我沒有因為我只是將相機演示給朋友，所以對設置的考慮不多。在這種情況下，ISO似乎處於較高水平，但其他場景的陰影更多：）

原始距離約為430米，因此我將這種作物縮小到原始尺寸的43％以進行模擬1公里後會是什麼樣子可以說，由於這種奇怪的比例因子，此結果比應有的結果更加模糊。

如果您覺得我可以識別的話認識那個人，也許她沒有戴眼鏡。但是，由於D750的“僅” 24 Mpixels，臉部的皮膚面積只有14像素左右。使用D810和相同的鏡頭，您可以輕鬆識別1.5公里（甚至2公里）外的朋友的臉。我希望有人進行測試：）

繼續進行演示...尼康P900具有16MP傳感器和83倍變焦。他們做了一些測試，不完全符合您的要求，但是非常接近。觀看視頻： https://www.youtube.com/watch?v=mRp13pRzzWQ

簡而言之，他們可以在大約1KM的紙上閱讀大字母。除此之外，事情確實有問題，並且縮放級別看起來像您無法輕鬆地挑選出一張臉。他們也有一些強制性的月球拍攝，但遺憾的是沒有很好地安裝相機。

相機鏡頭是一種望遠鏡。因此，它的已知分辨率極限等於λ/ D，其中λ是觀察到的光的波長，D是物鏡的直徑。所得值以角度單位而不是厘米為單位。

對於波長為580 nm的黃光，具有12厘米直徑物鏡的相機應具有約1弧秒的分辨率。

假設您需要在臉上至少50個像素才能拍攝出合理的照片，並且該臉的直徑約為24厘米（0.24 m），那麼使用 Wolfram a可以解決約1000米>。

很難說，但是在高山的某個地方，空氣可能足夠透明以接近此極限。